Simon Frankau's blog
Solving Rubik's Magic: Master Edition, Part 1: Group theory
In this post, I'm going to look at moving between the possible 6x2 flat configurations. For everything here, I'm assuming that you're viewing the Magic joined-up-rings-(starting position)-side-up. As the pattern's a bit distracting, I'll be using a schematic view of the Magic:
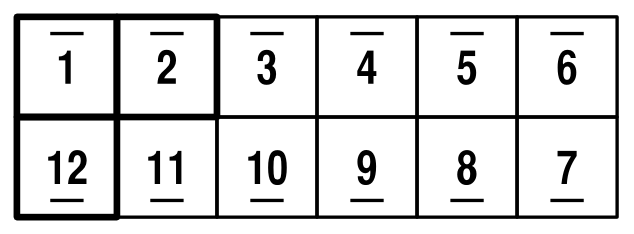
The numbers represent the position of squares initially, and the dots represent a particular edge. Initially, I'll place the dots on the outside, have the top-left square be square number 1. Note that the 3 highlighted squares in the top left more than define the position of everything else (see my previous post for details).
We're going to see what positions are reachable given combinations of three basic moves. The first, I'll call "X", after the way the squares windmill, and it's simply achieved by folding the Magic up, folding one square down, and another up:

X simply moves all the pieces around one step, without any rotation or fancy changes:
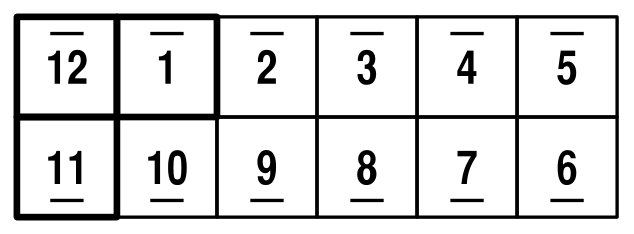
The next move, I'm going to call "O", since we make the Magic into a loop. Just fold the Magic in half, then slink it one square along. Note that it will then open up the other way:

So, this move can be used to change the orientation of the pieces:
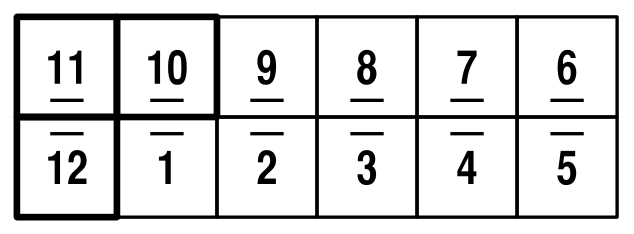
Note that so far, we can only rotate a piece by 180 degrees. Next move, I'll call "S" for "square", as we do a move that makes it into a square, then unfold it again (90 degrees around) to end up in a different shape:
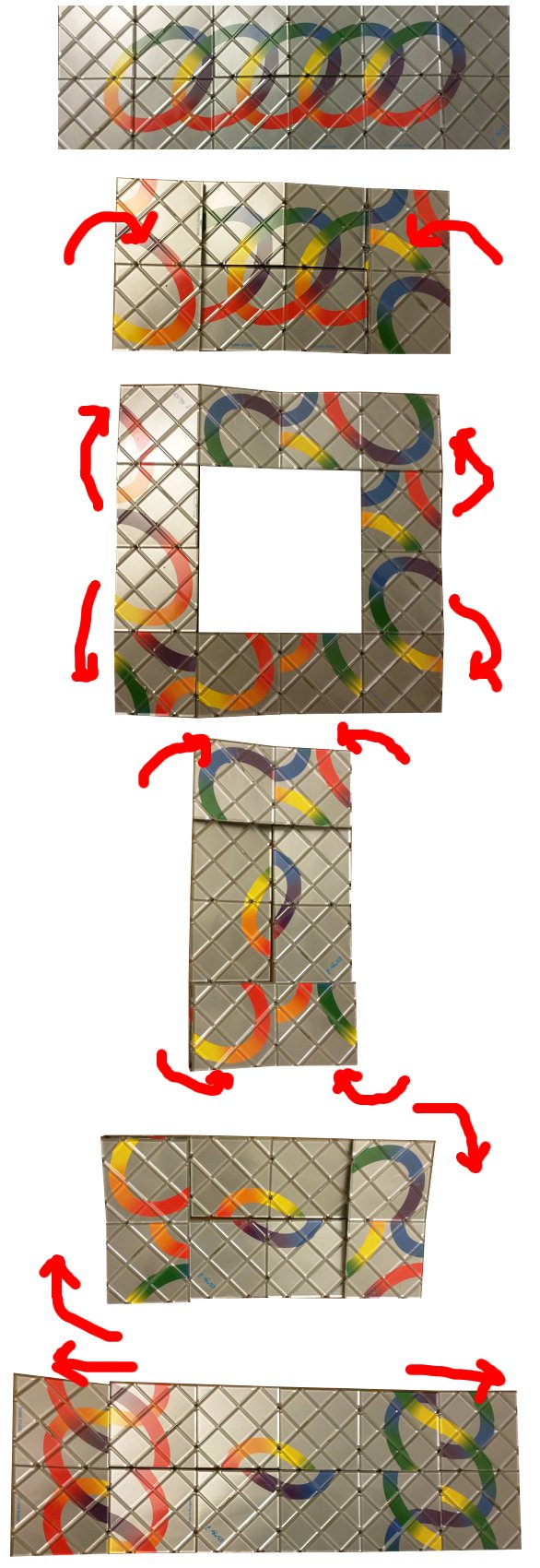
This move rearranges stuff quite a bit, and includes a quarter turn, which should allow us to reach more configurations:
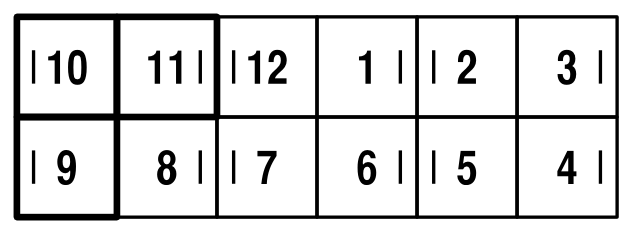
So, given these basic moves, can we create all configurations? Well, we can if we can move any piece number to the top left, rotate it arbitrarily and switch between clockwise and anti-clockwise numbering...
- Moving a piece to the top left Simply do "X" repeatedly.
- Rotate the top-left piece S, -X, -X, -X (-X being the undoing of an X move).
- Change direction of loop O, X, X (also rotates the top-left piece by 180 degrees, but you can fix that by doing the rotate step twice).
Given this, we can make any 6x12 configuration, so as long as we can go from a 6x12 to the final "W" shape, we can solve the puzzle. And that's the next post.
Posted 2015-07-04.