Simon Frankau's blog
Exponential back-off, revisited
The purpose of exponential back-off in retries is almost always to avoid overloading the target. Sometimes it isn't the case - for example excessive retries can drain batteries on the source side. Mostly, though, it's about avoiding an accidental DoS of the target, and so the back-off algorithm should be designed with that in mind.
Digging deeper, there are really two goals: Trading off not overloading the target with retries, versus retrying promptly after the service has come back. Exponential back-off has the nice property of making contact within a multiplicative factor of the outage duration. So, I'm not going to worry too much about prompt reconnection. I'm mostly caring about the "avoid accidental DoS" side of things, which is a real concern in large distributed systems.
Exponential back-off shouldn't be the only line of defense against this internal DoS, either. A comprehensive distributed system architecture should let you rate limit requests and drop traffic so that even in the worst case you can avoid your target getting overloaded.
Anyway, back to the chase: The primary purpose of exponential back-off is to avoid retries overwhelming the target service, prolonging an outage. This is why exponential back-off with jitter is so important. Exponential back-off alone ensures that the average request rate from retries decreases exponentially with time, but if all the clients saw the service go down at the same time, a pure exponential back-off will just lead to increasingly spaced-out huge bursts of traffic. Not helpful. The purpose of jitter is to decrease the peak loads down to a level where the target service can cope.
Therefore, the primary goal of our jittering algorithm should be to decrease the peak load on the target service, while ensuring retries are within exponential bounds (i.e. delays on discovering the service is up are controlled). Yet the common jittering algorithms don't make a decent attempt to meet this goal efficiently!
Let's take an example. We'll assume that all clients see the server go down at the same time - this seems pretty close to a worst case scenario for bursting retries. I'll use com.google.api.client.util.ExponentialBackOff as my implementation. This is not an unusual design, with a default multiplicative backoff factor of 1.5x, +/-50%. The retry pattern looks like this:
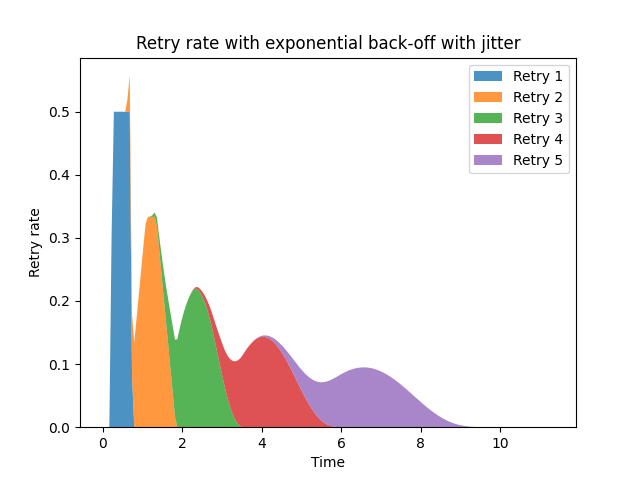
We can see the retries come in waves, with peaks. Each iteration of retries (after the first) forms a bell curve, overlapping the previous retry. These overlapping bell-shaped curves mean that the overall curve is very much not monotonically decreasing. The underlying service may reach a non-overloaded state, and then be pushed back into overload by the next peak.
To simplify things, let's look at Binary Exponential Backoff, as used by Ethernet. This uses discrete timeslots, a multiplicative back-off factor of 2, and a full randomisation range of 0-100% (i.e. retries occur after 0 to 2^n - 1 slots). The use in Ethernet is a bit different, since a single collision in a timeslot leads to failure, while we'd normally assume a service could handle rather more requests per slot, but we can still reuse the algorithm. What we see is this:
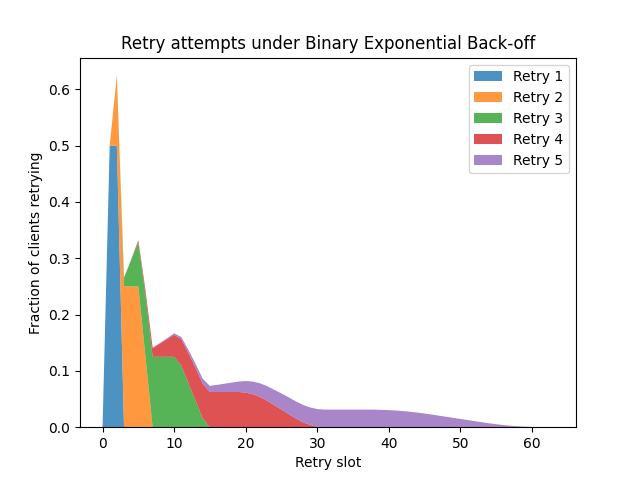
As the randomisation factor is now 0-100%, the distribution smears out much more effectively, with the distribution for each retry having wide, flat peaks. However, we still see local peaks caused by the overlapping generations of retries. What if retries didn't overlap?
This is what I've been thinking about with a modified binary exponential backoff. On the nth retry, delay some time between 0 and 2^n slots before retrying, but if the retry fails, wait until the end of that 2^n slot interval before restarting the timer, rather than doing so immediately. If you do this, the time from initial failure to (n+1)th retry is independent of the time to nth retry, and each retry lives in a separate interval - there are no overlaps. This produces a distribution that looks like this:
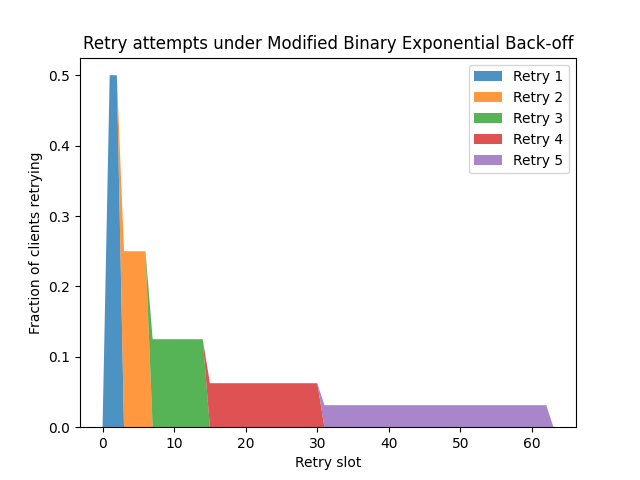
Unsurprisingly, the distribution is more stretched-out, since retry timers are started at the end of intervals, not immediately after a failure. However, the advantage is that, if all clients start retrying at the same time, we have a monotonically decreasing retry rate. It also feels a little fairer: If one client retried a bit earlier in one round due to chance, there's no bias to it retrying earlier in the next round.
We can see the difference between the distributions, and how the modified binary exponential back-off avoids spikes, in the following graph:
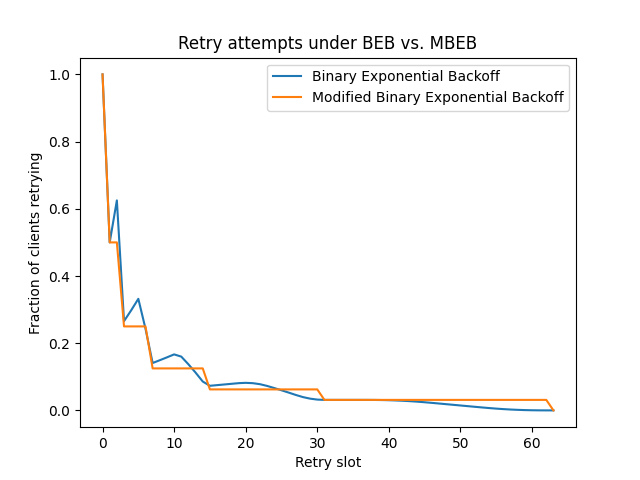
I'll admit that the difference isn't huge, and you can probably do more subtle and clever things than this simple modification. You could analyse the shape of the distribution if you don't assume all clients start retrying at the same time. Yet through all that I think this is a neat little improvement, and I'm rather surprised I've never come across it in regular introductions to exponential back-off.
Posted 2024-05-20.