Simon Frankau's blog
Ugh. I've always hated the word 'blog'. In any case, this is a chronologically ordered selection of my ramblings.
Good Stuff: Raspberry Pi and the iPhone
Looking at this blog, it seems I mostly complain about stuff. In real life, I'm not that bad (honest), but this is where I end up writing down various frustrations, and it's relatively rare that I actually want to point out good things. I thought I'd make an exception to my normal posting style...
Raspberry Pi is a fantastic project, aimed at getting children back into programming - the '80s BASIC-powered home computer for the new century. While there are a lot of people involved who I really respect and trust (including my PhD supervisor, and an ex-employer), it's really the brainchild of Eben Upton, who is a really great clever guy. I can't really say enough good stuff about it, so I'll give up now, and instead encourage you to go scour the web for more information.
From the very open to the very closed. I have finally bought myself an iPhone 3GS, after years of having the dumbest of phones. In the past, what I wanted was a small phone without all the pointless and expensive extras. Having had years of PDAs, I'd generally found them nice toys, but useless in practice. So, while I could see the use others were getting out of their smartphones, especially in mobile internet, I couldn't be sure it wasn't going to be another pile of wasted electronics.
It's been great. The main thing this gadget has provided, which the others haven't, is mobile internet. It does this well. However, either gadgets have changed, or I have, as I've found the organiser and notepad features very useful! I guess I've got more meetings and to-dos than I ever used to.
Why'd I get the old 3GS? Basically, I enjoy living on the trailing edge of technology. Every upgrade I do has the thrill of discovering the new features, just like everyone else, except the things I upgrade to are bedded down and reliable, and much cheaper than they would have been otherwise!
So, now that I own an iPhone, I can see what Apple are up to. The app store may be horribly closed, but their vision is compelling - they've managed something Microsoft never did, making their customers want a monopoly. Having skipped the painful early stages, I can also see why Apple held off on 'easy' things like multitasking and cut-and-paste for so long. The iPhone was their way of completely redefining the graphical user interface - challenging UI conventions that had basically been standardised on all platforms since Apple introduced them in the mid-'80s.
It's weird to see this 'phone interface', knowing it's also the basis for the iPad and the features are now making their way into OS X in Lion. Rolling out the features incrementally was Apple's way of making the world used to their new plans, and making sure they got it right, without assuming too much of the old ways. The fact that the supplied manual is really one sheet of paper, and the whole design is both so innovative and intuitive is quite amazing.
Posted 2011-11-14.
Retro-gaming Update: Chimera, AGC and Christminster
A while ago I had some nostalgia for a proper ZX Spectrum isometric game. So, I didn't do anything sensible, like play a classic such as Head Over Heels. No, I got a copy of Chimera, a budget label isometric game I played over 20 years ago. I never got very far with it, but that's probably because I was very young, right? I could beat it now!
As I have limited time nowadays, even with arbitrary save/restore, I felt I didn't have quite the edge to get through it and see how it panned out without a lot of pain, so I found a map and walkthrough. I followed it. It was clear that there would have been a lot of tedious exploration otherwise, creating my own map. It also soon became clear that the game design consisted of traversing a the longest routes the game designer could make, repeatedly. There are no actual moving baddies. Failure at the trial-and-error necessary to work out what does what leads to instant death and the going right back to the start. Fundamentally, the game is a race against the clock, but different events speed up the clock. For example, being in a room with a radiator seems to speed up the water clock something like a hundred-fold, thus totally unbalancing the game. It was so poorly set up that even with the walkthrough and map, and saving and restoring to optimise things, I still somehow managed to end up running out on the timers, and needing to use some pokes to complete the game.
Apparently I hadn't failed to complete the game because I was young. I failed to complete it because it was badly designed and tedious rubbish.
More rewarding have been the text adventures. After playing some commercial titles, I thought I'd try a couple of the more popular amateur efforts. I made my way through the Adventure Consumer's Guide, which was surprisingly fun. You get a sidekick who is vital to many of the problems, but also acts as a subtle hints mechanism. Mostly, however, the hints aren't necessary, since it's a fairly friendly game. As I said, lots of fun, and recommended.
Christminster is a bit of a classic in the 'IF' (interactive fiction) world. I'd tried to get into it a couple of times before, but never really clicked. The start, being a linear and not particularly helpful set of puzzles, had previously blocked me from exploring the game. So, I swallowed my pride and looked at a couple of hints. This allowed me into the main section of the game, and also gave me an insight into the author's mind, useful for solving following puzzles.
While there are plenty of puzzle components, and you're not lead round on rails, there is something of a plot to it, which makes a nice change from wondering around looking for a relatively unmotivated puzzle to solve. I'm now about halfway through (judging by my score), without having used any more hints, although I'm at a bit of an impasse now. Something to plug away at from time to time, I guess.
Posted 2011-09-27.
Pushchairs and geodesics
Maths abuse alert: All the following is done intuitively, and I've completely failed to formalise it, which is a bit embarassing given I've read a book on differential geometry.
It occurred to me the other day while wheeling the children to Greenwich Park, over the somewhat unever ground, that pushchairs try to follow geodesics. That is, if one of the wheels is taking a longer path, the pushchair will tend to turn away from that side. So, locally, it seeks a shorter path, and in the limit it'll run along geodesics.
Another way of looking it is that the pushchair will run along a path such that each side wheel runs along the same distance. So, along the path the derivative of distance stuff perpendicular to the path is zero, so that said distance stuff is locally maximised or minimised (and I guess we're looking at a minimum).
This in turn helped me understand a Feynmanism. Feynman said that light takes the fastest route between points, but I never really got why this should fit with the other formulations of the behaviour of light. However, I now see this is rather like the case with pushchairs. In refraction, light changes direction as it goes through media with different speeds of light, so that the wavefronts match up across the interfaces (GCSE description of refraction). In other words, it makes the light turn towards the faster medium, and away from the slower medium. And as long as it dos this in the appropriate way (which it does), once again it'll follow a geodesic. Lightbulb appears above my head.
Posted 2011-09-25.
On the Creation of Sentient Creatures
I watch far too much children's TV nowadays. This is a side effect of having children, I guess. There is a programme called 'Get Squiggling!', feature the character Squiglet, who can draw things and bring them to life, and have adventures with them. This includes drawing people, bringing them to life, and creating new sentient creatures out of nothing with no higher justification required than her own enjoyment. No serious thoughts about the implications, no ethics committee, no nothing.
I mean... I know it's a children's programme, and not meant to be taken deeply, but... surely the philosophical implications are huge?
Could you imagine the real-world consequences of people just being able to create new sentient, conscious beings without any real oversight? What a strange world that'd be...
Then I realised that's precisely the world we live in (and indeed the reason we have children's TV).
Posted 2011-09-11.
Choosing an Open Source Library
When developing code, you often want to glue in third-party components. If you're writing commercial software, and are pulling in commercial components, it's traditional for the manager deciding to be motivated by Fear or Greed. That is, to either buy from the biggest vendor (No-one Got Fired For Buying IBM), or the one offering the biggest freebies and kickbacks (a nice meal out with the vendors, you say?). Often the two factors point in the same direction, making the choice especially easy. The actual quality of the software can be completely irrelevant - it's basically marketing-driven.
When pulling in open source software, you can be properly objective, right?
So, what do you look at? You download the various alternatives. Read their docs, look at their APIs, build them and prototype with them. Perhaps look at the source to see what the quality's like. If one has a slight technical advantage, you'd probably go with that?
Wrong choice! You actually still want to go for something a little more like the PHB approach. Technical quality and appropriateness is still vital, but so is the community surrounding the software. You could argue that how they deal with bugs and support are parts of the technical quality, but that's missing the point. If you have to choose between two similar packages, don't choose the one with the minor technical edge, choose the one that'll be around in a few years' time!
What determines this? The momentum. Choose the one which is going places, with lots of happy contributing users, ongoing improvements, and fundamentally where the developers understand marketing. You're not using the product because you're a fool who is easily swayed by marketing, but because others are. It's a networking effect, and you want to be using the winning product.
As a clever developer, it's really cool to find an underdog project that's technically better than the obvious choice. It marks you out as part of the cognescenti. This can even be made to work - if it's technically much better, and you can support it yourself if it goes nowhere, or it's an underdog with clear positive momentum, it can be a good choice. Most of the time though, even in open source, the pure technical choice may not be the right one.
Posted 2011-09-11.
The English Riots: Business as Usual?
I have an amazing ability for waiting until a topic is no longer trendy before actually getting around to writing my thoughts on it. In this case, the riots in the UK. This means that reality turned out to match my thesis, even before I wrote it down; namely, that the riots didn't actually mean anything on a social or political scale. Having started with my conclusions, I shall move back to my reasoning...
I started thinking about how much it really meant when seeing reporting (a lot of it international) about how shocking this rioting was, and how it was revealing something fundamentally rotten in UK society, and should give those running the country pause to think. I even saw some comparisons with events in Egypt etc. (definite high clue quotient there). On the other hand, I'd also seen plenty of people writing it off as mindless thuggery, which is also a bit too convenient and stops any need to try to understand them. What's the actual situation?
First off, I'm ignoring the looting. That's not about the poor or underpriveleged. That's about a group of people where lots of people are clearly breaking the law, getting away with it, and gaining from that. Locally, different social norms start to apply, as following the law puts you at a disadvantage for no 'fair' reason. See, e.g. MPs' (MsP's?) expenses, phone hacking, etc. for other non-disadvantged groups doing similar things.
So, how many people were rioting, ignoring the looting? My opinion would be somewhat more convincing if backed up by real numbers, but it's clearly a tiny fraction of the communities, and looks not entirely dissimilar to the fraction of the population with a propensity to crime and violence anyway. There will also be some people carried along because they're normally only held back by fear of justice, and felt they could get away with it this time.
Put another way, the riots looked to me like people's normal behaviour, only condensed. Indeed, if you look at the amount of crime that was committed, I don't think you need to spread it out over an awfully long period before it blends into the overall crime level. It's certainly lost in the noise on the 30 year scale we seem to have between riots.
In summary, I don't think these riots mean nothing, they just tell us as much about the problems of society as our normal background level of crime and violence. Moreover, it's a real shame to focus on these riots when there have been so many much larger protests motivated by real issues. *sigh*
Posted 2011-09-11.
Oh, the Horror: Twitter
First, a couple of disclaimers:
- I understand the nature of start-ups. You quickly write rubbish code, because having something running is much more important than anything else. Moreover, the ideas are far more important than the technology details, and if you're successful you'll have plenty of time to rewrite later, right?
- This is Twitter Of Old. I'm pretty certain they've hired some people with actual technological skill and have real scalability now.
So, without further ado, I looked at some old presentations on Twitter's implementation and scalability. MY EYES! THE GOGGLES, THEY DO NOTHING! Let us remember that Twitter is a service so reliable that its most memorable image is the Fail Whale that appears every time it goes down...
So, in a presentation in the late 2000s, post-optimisation, they were handling 600 requests per second on 8 Sun boxes. That's 75 messages per box per second. Er, great. We best not talk about e.g. the performance expected out of IRC servers, a decade earlier.
The real killer for me was this quote:
For us, it's really about scaling horizontally - to that end, Rails and Ruby haven't been stumbling blocks, compared to any other language or framework. The performance boosts associated with language would give us a 10-20% improvement, but thanks to architectural changes that Ruby and Rails happily accommodated, Twitter is 10000% faster than it was in January.
This sounds really cool, until you realise that IN JANUARY, THEY WERE PROCESSING 3 REQUESTS PER SECOND. I've seen shell scripts with better performance, and they're all multi-millionaires now.
Not that I'm bitter. ;)
Posted 2011-08-24.
Simple Programming Advice: Put Examples in Comments
Just a quick note encapsulating some simple advice I'd only discovered recently: Put examples in your comments. Comments should add something to the code. Explaining what the code should do is good, how is bad, since the code itself should say how.
There's a school of thought that says that comments are dangerous, since they easily get out of sync with the code, becoming dangerous lies. So, don't comment, and make your code readable instead. I certainly have some sympathy with this viewpoint, but I think it's naive. For a sufficiently complicated algorithm, each step may be clear and well-named, but the overall structure and intention may still be mysterious. Very little code is designed to be readable by someone without an awful lot of context, and I think this is a real shame.
So, for comments to add value they should do something other than what the code does. A terse and formal description of what the function should do is well and good, but can sometimes leave the reader confused. By illustrating the same thing in another way, through some examples, you've got a much better chance of having the reader understand what you're up to.
The trendy programmer will point out that you can move the formal description of the function out into a set of pre- and post-conditions, and you can convert your examples into test cases. By doing this, you can ensure that your 'comments' never become out of sync with your code. In theory, yes. In practice, the Test Driven Development book made incredibly heavy weather of developing even the simplest of functionality, and I worry about how it scales up.
One day, maybe. In the meantime, comments explaining 'what' plus examples, please.
Posted 2011-08-24.
Programming "Experts"
Browsing Amazon's recommendations the other day, I saw "97 Things Every Programmer Should Know: Collective Wisdom from the Experts" by Kevlin Henney. Oooh, I thought, someone's managed to glue together a selection of blog posts (97 tips in one book aren't exactly going to be deep). As Amazon has "Look inside!", I did, and skimmed the table of contents...
I recognised several names. No, it's not a star-studded line-up. They've just contracted at my workplace. This is where the definition of "expert" comes in. They are, indeed, experts at discussing programming. They spend a lot of time at conferences, and networking with each other. They may know some language lawyering tricks. When it came to actual programming (or even design) I saw nothing setting them apart from most other seasoned programmers.
This is unfortunate, as in other domains I've met what I would regard as real experts. People who not only understand a subject backwards, but also have great and incisive ideas. This covers both proper academics and really effective business people. Those guys are a pale shadow of this.
This is not to denigrate the book - I suspect there are plenty of useful, non-controversial pieces of wisdom that deserve to be spread around and some of the contributors may deserve the title "expert". I guess I'm just complaining about my own naivety.
Posted 2011-05-21.
On symmetry-breaking, logic, perception and AI
One of the things I was thinking about recently was our perception of symmetries. For example, formal logics tend to have a symmetry between true/false, and/or, etc. Formally true and false aren't particularly distinguished, but they certainly have different meanings to us! This is one of those things that makes me suspicious of using formal logic as an underpinning of AI.
Are there similar isometries for natural languages? Could you switch other important concepts around, and a document remain just as consistent and useful? I don't think there is much of this. Why? Natural language is glued to the real world in a way formal languages aren't. When it comes down to it, language is bolted onto us as animals - there can't be the same symmetries amongst concepts that control life and death. In other words, perhaps a good way of creating an AI is to, say, base it around a program that wants to be happy! :p
Anyway, there are some symmetries in the real world, not just in language, but in our perception of the world itself. For example, I may perceive the colour red to look like what you think of the colour blue, and vice versa. As long as we're used to the colour schemes of the world, and have a consistent naming convention, we'll never know. Moreover, if my left-right perception of the real world were reversed, I'd have no way to tell. This one seems more odd to me, as there is (arguably!) an orientation to the real world, but I can never know if I'm seeing it correctly.
Despite these mappings of the real world to our perceptions being arbitrary, they're so taken for granted that people hardly notice they're there. What is the symmetry-breaking mechanism here? Is it really arbitrary? Are these different mappings truely isomorphic, or do the variations change our perception of the world? I have no idea!
Posted 2011-05-17.
Miranda Elizabeth Patricia Frankau
Miranda Elizabeth Patricia Frankau was born on Friday 6 May 2011 at 16:32, weighing 2950g (6 pounds 8 ounces). Mother and daughter are doing well, and the whole family are overjoyed. Yay.
Posted 2011-05-17.
Differential geometry, category theory and typing
NB: This entry involves hand-wavey maths-abuse.
I've been reading a book on differential geometry. It's the first maths book I've read (other than an introduction to category theory, which is kinda cheating) that actually has commutivity diagrams. I didn't really see why category theory might have come out of geometry, but it does seem far more understandable, having seen all these maps between different spaces, and mathematical equivalents of 'if you do this in over there, it's just like doing that over here'.
So, geometry's given category theory to computer science. I'd love it if computer science could give really clear types and anonymous functions to geometry. For example, what actually is a differential form? To keep it simple, let's look at a differential 1-form... these are standalone things like 'dx'. A-level maths said that a 'dx' isn't an actual thing, it's just a bit of notational convention in an integral, be careful, etc. At this level, it's made into a thing...
So, what is it? Let's say we have a manifold U. At each point of U we have a tangent space, which is a vector space of all the tangents at a particular point. How do we tie this tangent space to the underlying manifold? We can make it the space of functions which take derivatives in particular directions - i.e. the things normally written 'd/dx', for some direction x. That is, it's a vector space of functions from points to real values to points to real values. In Haskell type terms, this is a space of (Point -> Real) -> (Point -> Real). Given each point in U has its own tangent space, the overall type is Point -> (Point -> Real) -> (Point -> Real). Of course, in the text the parameters and abstractions and all the rest of it are done in implicit mathsy form, which I think makes things a little more obscure for no good reason.
What's a differential 1-form? It's a member of the cotangent spaces - the dual of the tangent spaces. Does this mean it's of type (Point -> (Point -> Real) -> (Point -> Real)) -> Whatever? No, it's actually a function from point to member of the vector space that is the dual of the tangent space at that particular point. In other words, this whole dual business is being done in a lifted world, if you were writing Haskell. The type is Point -> (Point -> (Point -> Real) -> (Point -> Real)) -> Whatever. What is 'Whatever'? Well, it's the scalar type of the vector space we're looking at, so for a fairly dull manifold, it'll be Real: Point -> (Point -> (Point -> Real) -> (Point -> Real)) -> Real. Still pretty impenetrable, but perhaps the start of an explanation.
What is 'dx' supposed to be? It's supposed to be the thing that when given a member of the tangent space projects out the d/dx component of it. How can we do that? Well, I guess we can just make a function which is linearly increasing in the direction of interest, but is otherwise flat, feed it into our derivative-taking function, and then evaluate it at an arbitrary point (the resulting function should be the constant function, for a given tangent space):
diff_1_form point tangent_space =
tangent_space_elt my_fn zero
where
tangent_space_elt = tangent_space point
my_fn = -- Function linearly increasing in our preferred direction
zero = -- Zero element of vector space
Other function could be substituted in, I guess. Is this correct and accurate, or have I missed something? I'm not sure. For all the formal notation, I'm still not sure if I've extracted the true meaning correctly!
Update! More re-reading reveals further details. The smoothly varying tangent space thing is called a vector field, and the point used to select the derivative-taking functor from the tangent space is the same point used to evaluate it. That is, the overall type is, depending on how you look at it, (Point -> Real) -> (Point -> Real), or Point -> (Point -> Real) -> Real - that is, you can look at it as a thing that transforms functions of the form (Point -> Real), or as, for each point in the manifold, a thing that maps functions to real numbers (specifically, the derivative of that function in a particular direction at that point).
Interestingly, the second type means that the tangent space is effectively over certain functions of the type '(Point -> Real) -> Real', which already looks like the dual of some vector space of functions of type 'Point -> Real'. Sticking together the element of the tangent space with the cotangent space is then basically the idea of passing this function to the tangent space functor. Indeed, the definition of the differential operator 'd' is exactly that:
Given a function f : Point -> Real, and a vector field X : (Point -> Real) -> (Point -> Real), d : (Point -> Real) -> ((Point -> Real) -> (Point -> Real)) -> (Point -> Real) is the surprisingly obvious ((d f) . X) x = X(f). (No, I'm still not sure I've got it exactly right!) For things beyond 1-forms it's more complicated.
Posted 2011-04-22.
The Universe as a Fixed Point
More random silliness. The common model of a the universe at a point of time seems to be based on the prevalent technology. So, in the mechanical past the universe is 'like clockwork'. Nowadays there is a bit more thought of the universe algorithmically - leading to things like Tiplerian nuttiness, The Matrix and Wolfram's New Kind of Science (I think - I've not read that tome).
A more general view is of the universe as the solution of equations. In some ways, this is not entirely dissimilar to the algorithmic view. For example, you can solve a PDE abstractly, or treat it as some kind of grid-based evolution of state. However, the equation solution approach is more powerful.
For example, you can be very silly, and extend the Tipler view. If the universe has infinite computational capability, it can simulate, say, the universe. Moreover, the universe we're in could be the result of some simulation. But we can go further than that, and have the universe simulate itself. That is, have the universe be a simulation running inside itself. This is obviously rubbish, if you treat the universe as a naive algorithm.
Another way of looking at it, though, is as a Y combinator attached to the world. That is, the universe is the fixed point of an equation of 'things that simulate themselves'. It simulates itself into existence. It's turtles all the way down. :p
Posted 2011-04-13.
Optimal memory reallocation
If anything is to demonstrate why I'm unsuited to blog-writing, it's the fact that I've been planning to write this post for about five years, and haven't done so because it's trivial!
When doing auto-resizing contiguous storage (e.g. C++'s std::vector), the normal growth mechanism is resizing by a multiplicative factor - e.g. doubling the size each time. My boss of 5 years ago pointed out that doubling is probably a bad factor. Imagine you have some kind of zero-overhead allocator, and this is the only allocation going on in your address space. The first allocation takes 1 unit, then 2 units, 4 units, etc. The next allocation takes 2^n units, but the sum of allocations so far take (2^n)-1 units. In other words, the new allocation must be placed in a fresh part of the address space, rather than recycling previously-used-and-now-free space. This can be viewed as rather wasteful (as such previous allocations are unlikely to be returned to the OS).
This got me thinking as to what is the optimal allocation resizing factor, in this rather simplified view of the world? We continue to assume multiplicative scaling. The array first takes 1 unit, the first resizing x units. The next resize can't go into the 1 unit space, so we tack x^2 on the end. However, we may be able to fit the next allocation (x^3) into the freed (1+x). Then we free the x^2, and x^4 goes in its place. x^5 is after that, and again we can hope to put the x^6 into the space previously occupied by (x^3 + x^4).
What x is appropriate? In both cases, the equation boils down to 1 + x = x^3. As I am lazy, I fed this into Wolfram Alpha rather than solve it myself. The solution by radicals looks ugly, so suffice to say the result is around 1.32. This is one of those cases where an approximation to e.g. 4/3 would be pretty pessimal, as the allocation then wouldn't fall into the pattern we're aiming for. Given the overhead of allocation, you're probably better off with a growth factor of 1.3 or maybe even 1.25.
At a scaling factor like that, you're going to be spending a lot of time copying data. The reallocation overhead may be a constant factor compared to getting the array size right in the first place, but that constant will be big.
What about if we're willing to do an extra step before we can start recycling memory? The real root of 1+x+x^2 = x^4 is just over 1.46. That's somewhat better. And if we're willing to do more and more steps, what is the limiting factor if we wish to eventually be able to fit the newly allocated array into some previously allocated memory? Why, the golden ratio, of course! (The limit is not a factor of 2, as it might look naively, since you have to keep the previous allocation until copying is complete)
All of this is somewhat silly and academic - in a real environment a growth factor of 2 is probably pretty reasonable in terms of avoiding unnecessary copying. On the other hand, from this we see that a growth factor of 1.5 might not be an unreasonable trade-off, in terms of reusing existing memory if you've got an appropriate allocator. A fun little toy.
Posted 2011-04-12.
Toddlers play Text Adventures
One of the odd effects of playing too much adventure games is that you can start to look at the world in odd ways. For example, it now seems to me that toddlers treat the world as a text adventure. David's common approach is to go through a think-do cycle, where the 'do' is generally a simple verb-noun phrase. Moreover, it genuinely does appear to be mostly adventure-game-like: Drop ball. Look. Get book. Examine book. Give book to daddy.
I guess it makes sense. After all, they're wandering around a strange world, where they don't know the rules, trying to make sense of it all. They have a limited interface to the world (a small vocabulary, both literally, and conceptually). As with most text adventures, communications with other characters is difficult.
So, my thesis is that randomly wandering around the house, moving objects about apparently aimlessly and doing wierd things isn't actually babyish at all! If an adult were dumped in a sufficiently alien environment, they could do no better....
Posted 2011-02-13.
Guild of Thieves
Having played Jinxster, I thought I'd have a go at another Magnetic Scrolls game. I tried to get into The Pawn, their earliest game, but got pretty much nowhere - it's lumpy and uneven. I'll probably complete it with a walkthrough for completeness' sake, but it's amazing how they developed in terms of playability. Guild of Thieves, being between the two in age, has a good pile of very reasonable puzzles, plus some really rough playability edges.
I've played it rather slowly and patchily, getting stuck and unstuck. One of the problems is realising when you've reached the endgame section. You have to keep checking if the bank is open now, so I'd been ready to start that section of the game for ages before realising I could! This is not made clear from the scoring system, which is pretty patchy, or the presence of a number of red herrings.
So, I resorted to a walkthrough to see what I'd been missing, only to discover... nothing up to the point I'd reached! Still, I was stuck on the coloured dice problem, and the banker's door, and getting impatient to finish, so I took hints to complete them. Not quite as even-handed as Jinxster, but pretty fair if you overlook a couple of flaws.
What next? A bit of Infocom?
Posted 2011-02-12.
Debugging is Computer Science
An awful lot of computer science has nothing to do with science - it's rather more like applied discrete maths. Oxford call their undergrad degree 'computation', and I have rather a lot of sympathy with this approach.
There are some parts of the subject which really are more like science, with experiments and stuff. Good systems design, for example, where benchmarks are created and implementations profiled, has a lot in common with setting up a lab experiment. However, this stuff rarely makes it into an undergrad course.
This perhaps explains why so few people seem to be able to debug properly, for debugging is science. Actually, it's worse than that. In science, you build a hypothesis, and then create an experiment that tries to disprove your hypothesis - if you can't, you have more confidence in your hypothesis. In other words, you start off with a consistent view of the world, and try to construct tests to extend your understanding. With debugging, your view of the world ('This should work') doesn't coincide with the reality ('It doesn't'). You have to design experiments to clarify where your view of reality differs from reality.
In short, in science you're testing hypotheses, in debugging you're testing assumptions. Either way, a scientific mindset is vital.
Posted 2011-01-21.
Happy Birthday David!
I don't tend to a) update this regularly, and b) write too much family-personal stuff. So, I shall belatedly state the obvious: David is now over a year old. Nearer 15 months now, in fact. It's been absolutely fascinating (and rather lovely) to watch him grow and learn. Observing him, it does make me rather suspect that all AI researchers have been barking up the wrong tree, but that's another story....
Posted 2011-01-20.
Fixing BoingBoing
I used to enjoy reading Boingboing back when it was a 'directory of wonderful things'. Nowadays there's more random pointless opinion pieces, mixed in with the cool things collected off the web. At worst, it's a left-wing new media Daily Mail. It's rather a shame, as they've also collected a couple of interesting new regular columnists.
One of the most tedious garbage-spewers is Douglas Rushkoff, who had an incredibly annoying guest column a while ago. He's back. So, I thought I'd finally work out how to do this GreaseMonkey-style filtering business. I finally managed to hide all articles mentioning him. I then tacked on a few extras. Between AdBlock and this script, and I now have something to remove all the most obvious rubbish from the site.
How's that for the Maker spirit?
Posted 2010-10-01.
Pseudocleverness
Time for another rant and a word I made up to describe a trait I particularly dislike. In a sense, it's experience/knowledge vs intelligence. Obviously the best kind of hire has both, but if you can only pick one I'd go for intelligence every time. When doing something new, it's intelligence that counts. If you're doing something again, knowledge or experience without proper understanding most likely means doing the same thing as last time, choosing a bad-fitting solution, and not learning from mistakes. So...
Pseudocleverness is what I'm calling the habit of suggesting a clever-sounding solution when the obvious, straightforward solution would do immeasurably better. The clever solution is never an original idea. It's a cool trick that has its place, which is then misapplied by someone who wants to show off, without actually thinking about the problem at hand and its suitability.
For example:
- Don't use stacks for storing your scoped data. Region-based allocators are very cool and efficient. Never mind that stack-based allocation keeps exactly the right amount of data around, has very good locality of reference, can be implemented in a few assembly instructions, and is pretty universally supported. If you're playing with continuations and closures you may want something different, but that wasn't what was under discussion.
- Don't use smart pointers in C++. Good design can control ownership explicitly, and anyway smart pointers can leak with cyclic references. We use smart pointers precisely because they stop the need for very careful design to control ownership. They are simple and straightforward, and pretty much universally used in the area that was under discussion. Those not using smart pointers aren't using them because they haven't started using them, not because they've switched away. In a new library planned for years of evolution where we have const data objects which form a DAG, not using a reference-counted shared pointers to manage the lifetime of these objects is nutty.
- When creating interfaces in C++, don't use abstract base classes. Instead, use complex templates to create tables of function pointers to non-virtual functions, making the interfaces rather more like traits on the objects. Fundamentally, reimplement virtual functions manually. 'nuff said.
Posted 2010-09-29.
Art in Summer 2010
It's that time of time of year again, so we've been doing our limited art seeing thing. Specifically, we went to the BP portrait competition at the National Portrait Gallery, followed by the Summer Exhibition at the Royal Academy, both of which I tend to enjoy. David came along, and was wonderfully quiet throughout (sleeping through most of the RA!).
The portait competition was happily a bit more varied than last year. Not so much in the way of photo-realism, so there was a bit more opportunity for personality to be expressed. There were a few I didn't care for, but on the whole I really rather enjoyed it.
After brunch at the NPG's rather nice restaurant, we decided we'd attack the Summer Exhibition. We wondered if they'd cope with a push-chair, but it turned out to be fine. Critics have panned it, but I enjoy it pretty much for the same reason as they hate it. I love looking through the higgledy-piggledy of the entries from the hoi polloi in the Weston rooms, and I enjoy looking on in horror at the overpriced rubbish from the more famous artists (special prize here for Tracy Emin's awful, awful tat). Generally, though, I enjoy trying to find those few items I think utterly lovely.
The prices have rather increased this year - what that's doing with a recession, I don't know. So instead of looking at my favourite things that are almost on the edge of affordable (ha!), I thought I'd just ignore price and list my favourites:
- River Flood - Antony Whishaw RA Wonderfully atmospheric abstract painting.
- Personal Creation Myth - Grayson Perry How he produces such beautiful, yet disturbed objects, I have no idea.
- Blue Hold - Elizabeth Magill A moody and desolate picture of some trees, somehow brought to life by bright yellow paint. Much more lovely than it sounds. She won the 'Sunny Dupree Family Award for a woman artist' award, which seems almost offensive to me, since its loveliness seems entirely independent of the gender of the painter...
- Einschuesse - Anselm Kiefer Huge, looming and highly textured oil painting. A huge grey mountain and fields, with sinister red spots. The title appears to be 'bullet hole'.
- Various Fred Cumings Four rather nice landscape paintings.
Posted 2010-07-19.
Electronics for Newbies: Oscillator practice
Some people might suggest that the theory of crystal oscillator design should perhaps precede constructing such an oscillator. I thought a) I'd have a go by doing, and b) It's easy, anyway, right?
Consulting Horowitz and Hill plus a minimal bit of research on the internet indicated that I wanted a Pierce oscillator, that you need to get capacitors which match the crystal, and that otherwise the series and feedback resistor hardly matter.
So, I got myself a 4MHz crystal and 32kHz crystal, both with their appropriate capacitors. I used a 10k series resistor, and a 10M feedback resistor. I breadboarded up the circuits, attached my 'scope and... nothing. Hurrah. The 4MHz generated nothing, and the 32kHz generated noise.
So, I lightly investigated the theory, to see which tweaks might make the things work. The 4MHz crystal wasn't too difficult to twist into working. Replacing the 10k series resistor with 220 Ohms (!) made it work, at least some of the time. 220 Ohms is about all I have, otherwise, as most of my resistors are either pull-ups, or current limiters for LEDs - That's all I needed for simple logic circuits, I thought. Either way, it worked, as can be seen in my little picture.
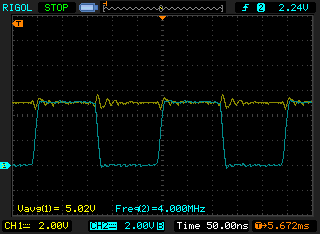
The yellow trace is the power supply. Perhaps I should have put more decoupling in? I'll experiment later. My skimming of the internet, trying to find clues as to the problem lead me to a couple of useful application notes - Microchip's AN849 and ST Microelectronics's AN2867. The former seems to concentrate on debugging broken oscillators, while the latter on using maths to design them right! In my current situation, the former was what I approached first. With the small resistor, I was worried about overdriving, so I moved the resistor to the other side of the capacitor and measured either side of it to get the potential across it (using the exciting 'maths' mode of my 'scope).
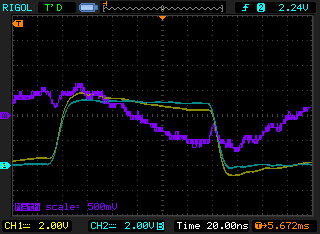
It looks like it could be just a little overdriven, or it could just be the way I'm measuring. Of course, measuring all this stuff with an oscilloscope probe is rather fun, since the probes have similar capacitance to the caps actually designed into the circuit! The other fun point is that as it's really just a little feedback circuit, with different gains at different frequencies, the oscillation in a badly designed circuit (e.g. mine) can vary on a per-startup basis. Sometimes there might be no oscillation, and at other times a different mode may appear. I have much to learn!
Finally, I tried my hand at getting the 32kHz crystal working, which had been much more uncooperative. With much faffing, I got it to work (unreliably) with 18pF capacitors, 30M of feedback resistance, and 115k of series resistance. As you can see from the screenshot, it's incredibly noisy. Next stop, I'll look up the theory and do some maths to see if I can make it work better!
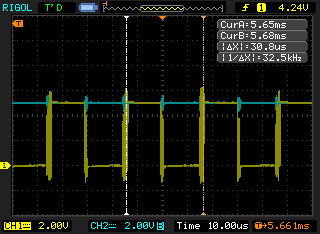
Posted 2010-06-27.
Electronics for Newbies: Oh, silly scope
David L. Jones apparently has too much influence on my life, as for my birthday I got one of those lovely Rigol oscilloscopes. It's still not modded to 100MHz, as I'm not playing with those kinds of frequency. Indeed David Frankau's also having a huge influence on my life (unsurprisingly), since I've hardly played with it, and my birthday was more than 2 months ago.
Still, the use I've had out of it has been terribly helpful. Starting off, I can see the bouncing when I flip a switch, or the logic delay propagation through a chip. I've got a photo of the latter, which just happens to show off my new pride and joy.

Really, though, it's been most useful when debugging, of which I've done more than anything else recently. As a demo, I've now got lovely little screenshots of my wallwart power supply's output, before and after smoothing.
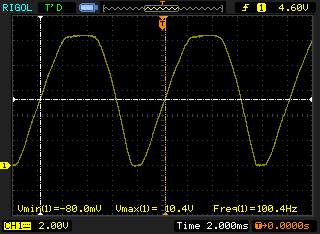
It's interesting to see the way the rectified waveform doesn't have a massively sharp bounce, and the top of the waveform isn't super-smooth-and-symmetrical. Once I've added a smoothing cap, all that's left is a little ripple - about half a volt by the looks of it.
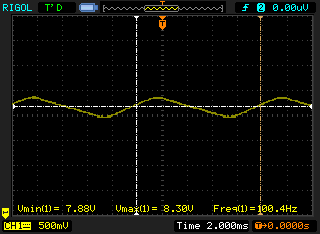
Lovely. Then I tried to show the result of regulation with the MCP1826S. Mucho weirdness. The output level was about right, but it was somehow pulling the input voltage way down, too. And this was with a very light load. That's not right, is it? Hmm. It's getting really hot, too. Since I'm using the dual channels of the scope as voltmeters, it frees my actual multimeter up to measure the current. Several hundred milliamps. That's really not good.
It's pretty happy when I run it off an old 9v battery, but this mains supply makes it go nuts. What does this tell me? It tells me to read the data sheet properly! While these regulators are nicely low drop-out, and are capable of driving pretty big currents, they can only take 6V in. That may be useful for driving low-voltage circuitry, but it seems a little lame for what a 5V regulator can handle. Silly me for not reading the datasheet, and after I've stuck 12-13V across them I'm now left with a couple of TO-220-packaged heaters. They certainly don't do a sensible job of regulation any more.
Anyway, now that I have a little more experience with oscilloscopes, I think it's time for me to go off and play with crystal oscillators....
Posted 2010-06-27.
Bureaucracy and Broken Hinges
From time to time, I try to keep up my text adventure habit. After a period of being stuck in Guild of Thieves I decided to have a go on the Infocom side with Bureaucracy, which has the added advantage of having had Douglas Adams's input into it.
It's a fun enough game. The plot does have Adams's fingerprints on it, and the puzzles are varied and interesting. However, I think I've been spoilt by Magnetic Scrolls! I'm not too worried by the lack of pictures, but Bureaucracy is comparatively... spartan. The descriptions are short, the number of locations limited, and the structure quite linear. To compare, the total points in the game is 21, versus 500 or so for some other adventures. Admittedly, it gives out points one at a time, rather than in lumps of fives or tens, but this is still small.
Difficulty-wise, Bureaucracy is reckonned to be rather difficult. I found it straightforward with lumps of difficult. Of the twenty or so puzzles in the game, I got stuck on three. As I'm annoyingly time-limited nowadays, I resorted to spoilers. Rubbish me! Reading the answers generally made me feel rather silly - I should have got them! On the other hand, they really weren't straighforward. The game's sadistic sense of humour stretches to the puzzles. You might see how to solve a puzzle, but it'll set an obstacle in the way, and another. Oh, and the puzzle may involve an item from way earlier in the game you didn't know you needed. Nice.
Still, it really was a good pile of fun.
In other news, my MacBook Air continues to give hardware problems. I think the warranty-expiration timer must have fired. Closing it, the hinge made a funny noise, and it failed to shut. Further inspection revealed that the little metal bits had, well, kinda got out of sync. A bit of fiddling did get them back. However, the hinge cover ('antenna cover') is plastic, and the dislocated metal was levered into it, weakening the plastic. It's now broken, leaving a little hole in the hinge area. I think it provided a certain amount of pressure on the hinge, so the hinge is now a little weaker, and the screen tends to fall back.
Looking at the internet, I don't appear to be the only one - see here, for example. The replacement parts are hideously expensive, and to fix it involves removing pretty every internal component. I think I'll hold off for a while, after the last fix....
Posted 2010-06-06.
Return of the Mac
Hurrah! My Macbook Air is finally fixed! And it only took a month... The hard drive died when we went on holiday to Cheltenham (apparently it's still a bad idea to travel with them in suspend mode - I thought things like that were pretty ok, now?). Fortunately, the failure mode was that it eventually succeeded when doing most reads, so I managed to back up most of the stuff I wanted after the event.
Things I have learnt include:
- Back-ups are useful.
- When making disk images, large archives, etc., avoid FAT32, as files only go up to 4G. Useful.
- Apple's disk imaging software is a big girl's blouse in the face of read errors. Log the error, skip the sector and carry on? Ha! Give up immediately? Of course!
- Caroline relies on the internet an awful lot.
- Using a computer connected via the telly is really a lot less convenient than a laptop.
- Official Apple repairs are expensive.
- Even unofficial SSD storage is still eye-watering in price.
- You can buy pretty much anything off e-bay, but it might take some time to arrive if there's a cloud of ash in the sky.
- The innards of Macbook Airs are fiddly...
- But actually straightforward enough to deal with, given instructions off the internet, and a brand-new Philips #00 screwdriver.
Posted 2010-05-08.